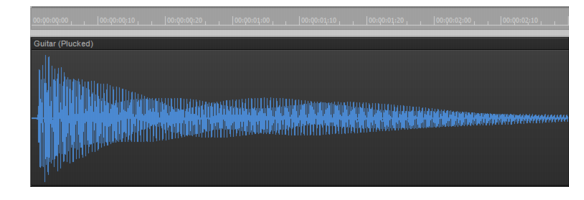
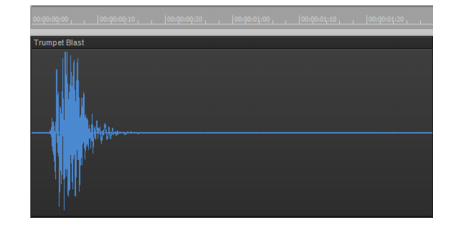
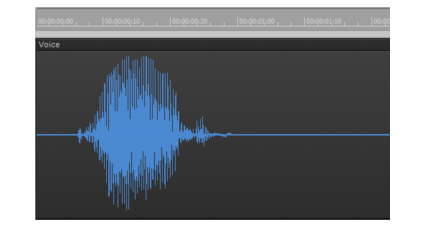
A sound wave can be represented in many different ways: as a mathematical formula, as a series of numbers, or graphically as a waveform. A waveform displays the size, or amplitude, of the vibration as a function of time. For example, the waveform of the sound of the plucked guitar string might look like this:The center line of a waveform is the zero line; it corresponds to the rest position (displacement of 0) of the original vibrating object. (A waveform for perfect silence would be a horizontal line at zero.) Back and forth motions of the vibrating object translate to upward (positive) and downward (negative) excursions of waveform amplitude. For example, a close-up of a portion of the guitar waveform might look like this:The waveform crosses the zero line twice during each complete vibration. These zero-crossings are important in digital audio processing; they are good places to cut waveforms apart and splice them together. If waveforms are cut or spliced at other locations, clicks and pops can occur. The maximum amplitude of the waveform in each vibration is also important: it determines the strength of the vibration, and thus the loudness of the sound.
Tip - Searching Documentation
Tip: To search for a specific topic, type your search query in the Search Cakewalk.com field at the top right of this page.
When the search results appear, click which product's documentation you would like to search to filter the search results further.
Note - Using Offline Help
Note: If you prefer to always use offline Help, go to Edit > Preferences > File > Advanced in your Cakewalk software and select Always Use Offline Help.
If you are not connected to the internet, your Cakewalk software will default to showing offline help until an internet connection becomes available.